矩阵行列式瞬秒立体图形体积计算

Note

本文原作者：JustPureH2O

原文地址：https://justpureh2o.cn/articles/42897/

行列式概念&几何意义

行列式最初作为判断某个方程组是否有解的依据被人们使用，记作 \(\det\)，有时也用形如 \(\left|\begin{matrix}a_1&a_2&a_3\\b_1&b_2&b_3\\c_1&c_2&c_3\end{matrix}\right|\) 的式子来表示这个矩阵的行列式的值。类比一元二次方程的 \(\Delta\) 判别式——我们定义，当矩阵 \(A\) 的行列式的值为零时，该矩阵方程组无解，即 \(\det(A)=0\) 时方程组无解。

对于一个矩阵，它的行列式计算方式为按行/按列余子式递归展开。何为余子式？来看一个例子：

例如矩阵 \(A=\begin{bmatrix}1&4&8\\2&0&-1\\6&-4&10\end{bmatrix}\)，其余子式 \(M_{n,m}\) 定义为删去元素 \(a_{n,m}\) 所在行和列的所有元素后原矩阵余下部分组合成的新矩阵。在本例中，我们删去第一行和第二列（\(a_{1,2}\) 所在行与列），得到 \(M_{1,2}=\begin{bmatrix}0&-1\\-4&10\end{bmatrix}\)；类似地，\(M_{3,2}=\begin{bmatrix}1&8\\2&-1\end{bmatrix}\)。

\(n\times n\) 方阵的行列式的计算公式在下面给出：

\[ \det(A)=\sum\limits_{i=1,j\in[1,n]}^{n}(-1)^{i+j}a_{i,j}\det(M_{i,j}) \]

当矩阵通过余子式的递归化为二阶时，行列式可以直接用主对角线元素的乘积减去副对角线元素的乘积得到。即对于 \({2\times2}\) 方阵 \(A=\begin{bmatrix}a_{11}&a_{12}\\a_{21}&a_{22}\end{bmatrix}\)，\(\det(A)=a_{11}a_{22}-a_{12}a_{21}\)。根据公式，行列式可能出现负数，但只要行列式非零，方程组就是有解的。

而在几何方面，行列式用来描述一个线性变换对体积造成的影响。空说无凭，我们先找一个简单的 \({2\times2}\) 方阵来演练一下：

假设两个不共线、共起点的二维向量分别是 \(\vec a=(1,2)\) 和 \(\vec b=(4,1)\)，它们围成的平行四边形如下图：

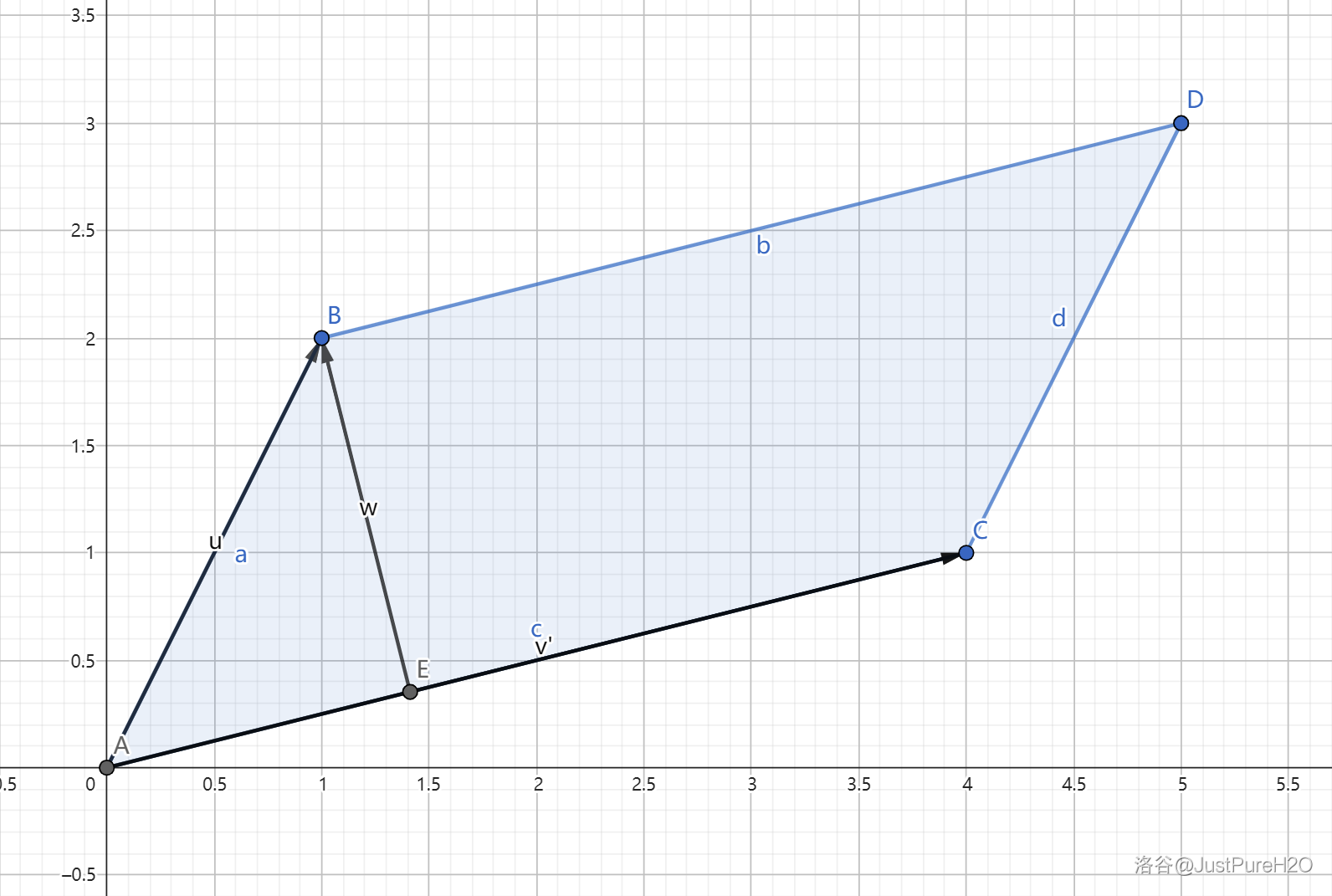
假设 \(\angle BAC=\theta\)，那么

\[ S=|\vec{AC}||\vec{AB}|\sin\theta=|\vec{AC}||\vec{AB}|\sqrt{1-\cos^2\theta}=|\vec{AC}||\vec{AB}|\sqrt{1-(\frac{\vec{AC}\vec{AB}}{|\vec{AC}||\vec{AB}|})^2} \]

用向量代入，得：

\[ \begin{aligned} S&=\sqrt{(a_x^2+a_y^2)(b_x^2+b_y^2)}\sqrt{1-\frac{(a_xb_x+a_yb_y)^2}{(a_x^2+b_x^2)(a_y^2+b_y^2)}} \\&=\sqrt{(a_x^2+a_y^2)(b_x^2+b_y^2)-(a_xb_x+a_yb_y)^2} \\&=\sqrt{a_x^2b_x^2+a_x^2b_y^2+a_y^2b_x^2+a_y^2b_y^2-a_x^2b_x^2-2a_xb_xa_yb_y-a_y^2b_y^2} \\&=\sqrt{a_x^2b_y^2-2a_xb_xa_yb_y+a_y^2b_x^2} \\&=|a_xb_y-a_yb_x| \end{aligned} \]

当我们把两个向量以如下的形式放入一个矩阵中，奇迹发生了：

\[ A=\begin{bmatrix}a_x&a_y\\b_x&b_y\end{bmatrix} \]

此时 \(\det(A)=S\)。平行四边形的面积就是这个矩阵的行列式的绝对值！

平面图形的面积

事实上，上面介绍的行列式实际上计算的是给定向量围成的图形的面积。对于两个不共线、共起点向量，它们会围成一个平行四边形，而它的面积可以直接由 \(\left|\left|\begin{matrix}a_x&a_y\\b_x&b_y\end{matrix}\right|\right|\) （行列式的绝对值）计算得来。

那如果是一个三角形呢？

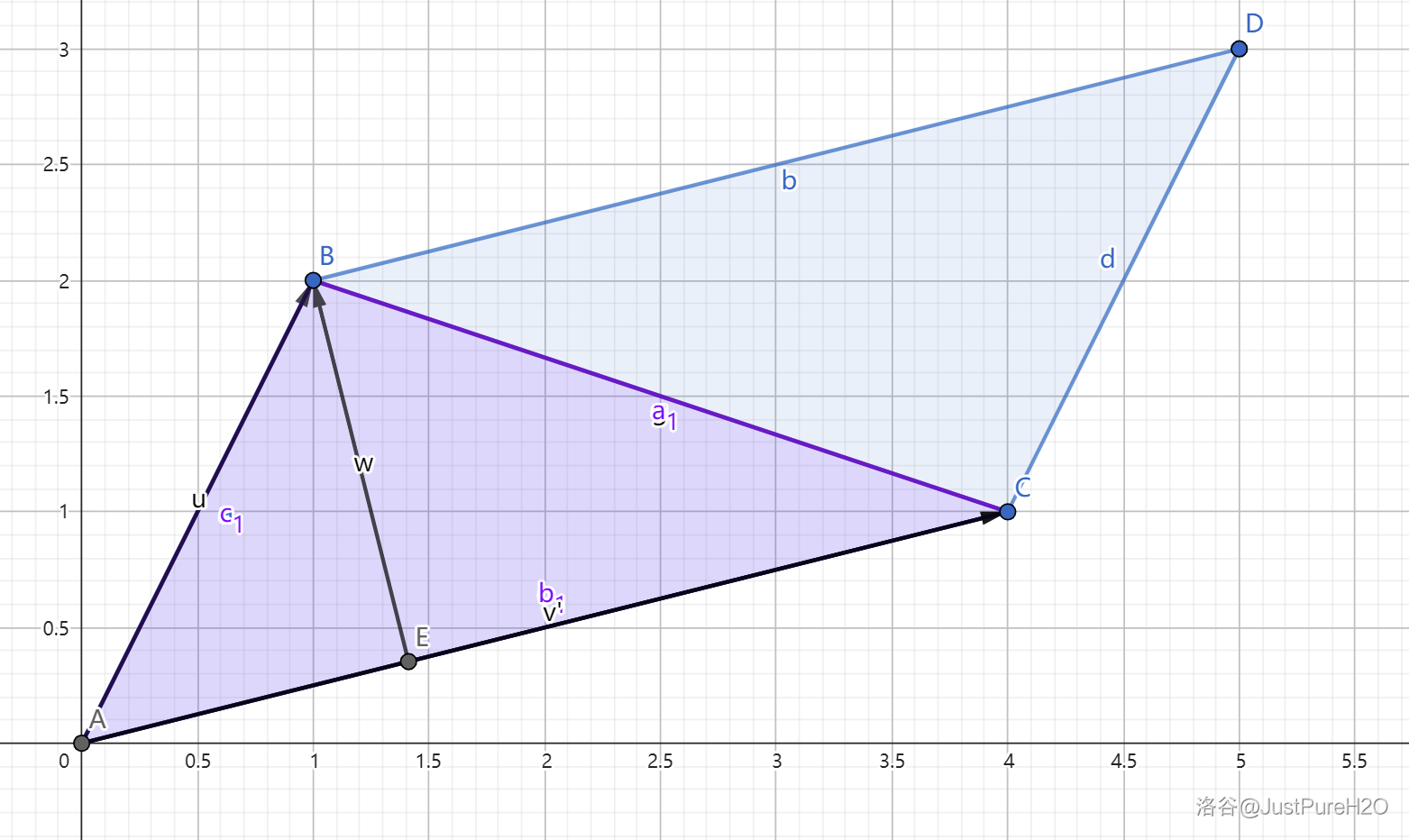
发现三角形恰好占据平行四边形的一半空间，面积就刚好是整个平行四边形的一半，因此 \(S_{\triangle ABC}=\frac{1}{2}\left|\left|\begin{matrix}a_x&a_y\\b_x&b_y\end{matrix}\right|\right|\)。\(\triangle BCD\) 的面积同理，\(S_{\triangle ABC}=S_{\triangle BCD}\)。

如果是一个正六边形：

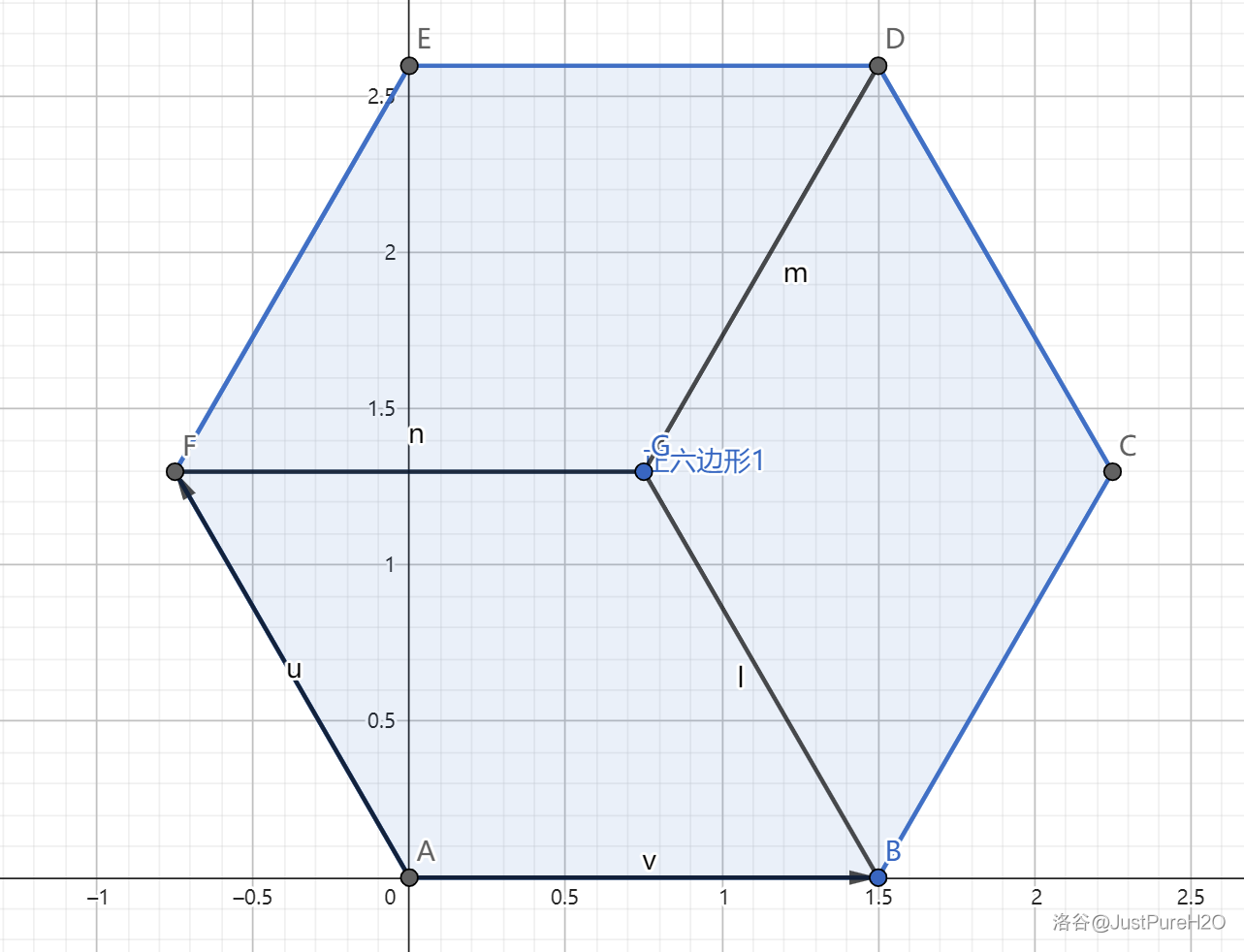
可以发现一个正六边形是由三个这样的平行四边形组合得到的，因此 \(S=3|\det(A)|\)。对于平面图形的面积计算，重点在于找到组成这个图形的单位平行四边形，找到后直接用行列式乘以响应倍数即可。

立体图形

我们首先从三棱锥开始。不难想象，三个不共线、共起点的三维向量会围成一个平行六面体。那么这个三棱锥放在这个平行六面体中，它会占据平行六面体恰好 \(\frac{1}{6}\) 的体积，如下图：

三个相同的三棱锥恰好占掉这个平行六面体一半的体积，那么三棱锥的体积就是整个平行六面体的六分之一。根据前文所述，我们把围成这个平行六面体的三个三维向量排成一个 \({3\times3}\) 方阵 \(A=\begin{bmatrix}a_x&a_y&a_z\\b_x&b_y&b_z\\c_x&c_y&c_z\end{bmatrix}\)。三棱锥的体积就是 \(V=\frac{1}{6}\left|\left|\begin{matrix}a_x&a_y&a_z\\b_x&b_y&b_z\\c_x&c_y&c_z\end{matrix}\right|\right|=\frac{1}{6}|\det(A)|\)。

例题演练

例 4.1（《步步高一轮复习83练 2024人教A版》P355 T6）

在正四棱锥 \(P-ABCD\) 中，\(AB=2\)，\(E,F,G\) 分别为 \(AB,PC,AD\) 的中点，直线 \(BF\) 与 \(EG\) 所成角的余弦值为 \(\frac{\sqrt6}{3}\)，则三棱锥 \(P-EFG\) 的体积为？

这道题来自于我一轮复习学案里的某道题目，当时用常规方法算半天就是有一个小三棱锥体积算不出来，导致这道题做（蒙）错了。现在用线性代数来解就非常轻松快速了。

给出题图：

总结一下，我们只需要知道某个几何体的一组共起点、不共线的边向量，就可以算出这个几何图形的面积/体积，所需向量的数量和图形的维度是一致的。