\(\texttt{0x00}\) 写在前面
没想到退役之后一重返 whk 就被这玩意儿困扰得苦不堪言……所以现决定将这一整个知识框架全部重新补一遍。
首先得知道圆锥曲线的定义:(因为怕自己理解的不严谨就搬运了)(from 百度百科)
圆锥曲线,是由一平面截二次锥面得到的曲线。圆锥曲线包括椭圆(圆为椭圆的特例)、抛物线、双曲线。起源于 \(2000\) 多年前的古希腊数学家最先开始研究圆锥曲线。
圆锥曲线(二次曲线)的(不完整)统一定义:到平面内一定点的距离 \(r\) 与到定直线的距离 \(d\) 之比是常数 \(e = \frac{r}{d}\) 的点的轨迹叫做圆锥曲线。其中当 \(e > 1\) 时为双曲线,当 \(e = 1\) 时为抛物线,当 \(0 < e < 1\) 时为椭圆。
定点叫做该圆锥曲线的焦点,定直线叫做(该焦点相应的)准线,\(e\) 叫做离心率。
为什么写这篇文章(Why)
哲学上讲分析原因要从多方面来思考,所以我也进行了如下~根本不正经的~思考:
必要性:
理论必要性:
圆锥曲线位于选择性必修一,是高中数学进入选修之后的第一道难关,也是学好解析几何乃至整个数学学科的基石,可以说,学不好圆(元)曲,高考数学基本无缘 140pts。
实际必要性:
高考大题中至少有一道圆锥曲线是毋庸置疑的,而且选填也是压轴般的存在,平均下来一套试卷占分 25pts 左右,并且其中的~形而上学~代数成分极多,对于提升计算力和观察力有很大帮助。
重要性:
这次期末统考因为圆曲大题考了两道,两道的最后一问都没时间算了,所以喜提 135pts 的坏成绩(呜呜呜,下次再也不敢了)。
综上所述,补习圆曲,急不可待!
然而光有了 motivation(动机)还不够,还得有方法。
怎么学(How)
学习圆锥曲线,首先就得深刻了解他们各自的定义,比如双曲线就定义为:与两个固定的点(叫做焦点)的距离差是常数的点的轨迹。这里比较容易忽略的一点是:得看是否加了绝对值,若有,则是双;若无,则是单。
了解好圆锥曲线的定义是非常关键的一步,这决定了基础,也为后来的各种二级结论做好铺垫,毕竟各种二级结论都是以她们为基础的。
关于二级结论便不妨让我废话两句。
鲁训曾经在他的《呐喊吧!我的圆锥曲线!》自序中写道:
“假如一道圆锥曲线大题,是绝无捷径而万难计算的,考场里有许多红温的人们,不久都要算死了,然而是从绝望入死灭,并不感到就死的悲哀。现在你大嚷起公式来,惊起了略懂二级结论的几个人,使这不幸的少数者来受无可挽救的临终的苦楚,你倒以为对得起他们么?” “然而几个人既然起来,你不能说决没有做出这大题的希望。”
----鲁训《呐喊吧!我的圆锥曲线!· 自序》
由此我们可以看出,学习圆锥曲线最重要的不仅是基础的定义,还有二级结论。但是二级结论也不能盲目地记忆,还要对她是怎样推理出来的心知肚明。
当然,除了以上两个学习方向,更少不了的是自己一步一步认真地计算以及对各种题型分类寻找共同点和思路切入口,以提高对各种题型的洞察力和做题效率。
这篇文章写什么(What)
根据“怎么学”的内容,这篇文章主要介绍定义,各种二级结论以及证明,至于个人总结出的看题、做题的坑点、切入点、思考点和小技巧,就留到下篇。
你现在应该对这篇文章有大概的了解了,那么,开始吧!
\(\texttt{0x01}\) 椭圆
0. 基本代数形式
横椭:\(C:\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1(a > b > 0)\),焦点在 \(x\) 轴上。
竖椭:\(C:\frac{y^2}{a^2} + \frac{x^2}{b^2} = 1(a > b > 0)\),焦点在 \(y\) 轴上。
\(a^2 = b^2 + c^2,0 < e < 1\).
1. 基本三大定义
第一定义
平面内动点到两个定点距离之和为定值的动点的轨迹。
形式化的,若 \(|PF_1| + |PF_2| = d = 2a\),则 \(P\) 的运动轨迹为椭圆。
这个定义是最基础的定义,也是数学书上讲的,唯一的一种定义,而其后的两种定义都未出现在教材中,高考不能直接写。
同时这也是椭圆中最重要的定义,因为很多二级结论都是可以根据其推理出来的,包括第三定义。
第二定义
椭圆上的点到焦点的距离与到准线的距离之比为离心率,对椭圆来说,其准线为 \(x = \pm\frac{a^2}{c}\).
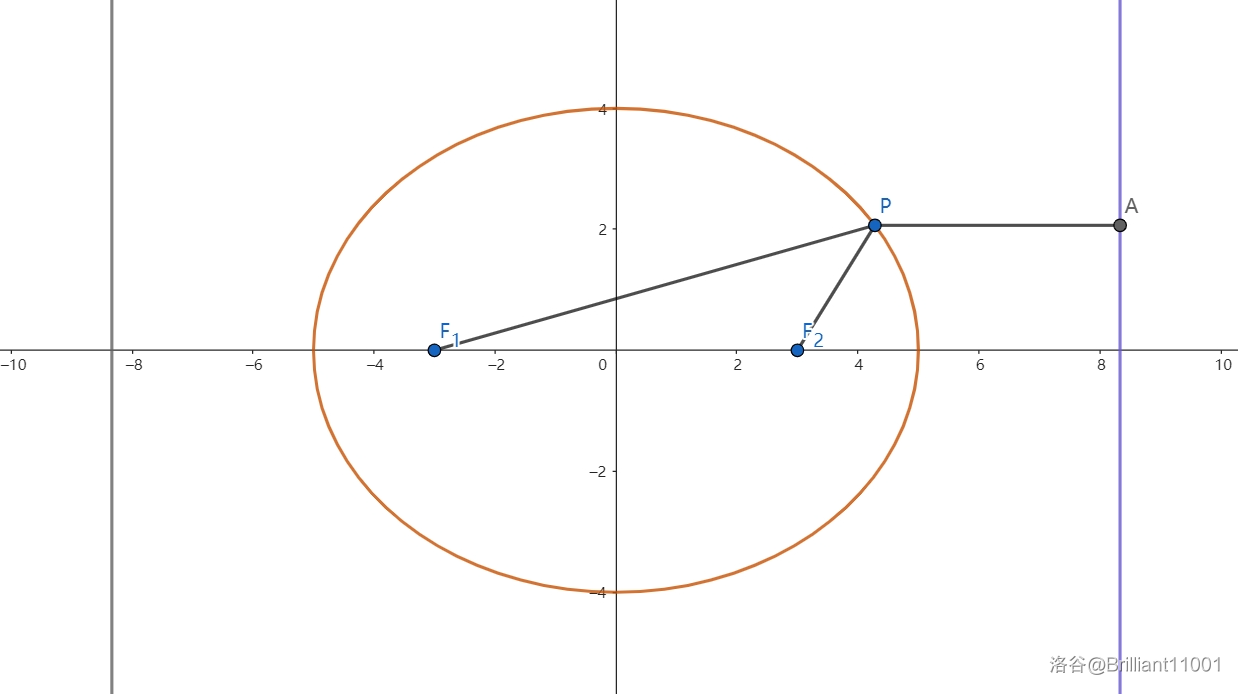
如图所示:其中 \(\frac{PF_2}{PA} = e\),契合了圆锥曲线的普遍定义。
设 \(P(x_0, y_0)\).
通过第二定义我们可以推出著名的焦半径公式:\(\begin{cases}PF_1 = a + ex_0\\ PF_2 = a - ex_0\end{cases}\).
推导:
设 \(P(x_0, y_0)\),那么根据第二定义得:
\(\frac{PF_2}{h} = e\Rightarrow \frac{PF_2}{\frac{a^2}{c} - x_0} = e\Rightarrow \begin{cases}PF_1 = a + ex_0\\ PF_2 = a - ex_0\end{cases}\).
记忆口诀:左加右减。
但是很遗憾,因为之前提到高考是不能直接用这个定义的,那么如何用第一定义来证明呢?
推导:
设 \(P(x, y)\),则:
\(|PF_2| = \sqrt{(x_0 - c)^2 + y^2} = \sqrt{x_0^2 + c^2 - 2x_0c + b^2 - \frac{b^2}{a^2}x_0^2} = \sqrt{\frac{a^2 - b^2}{a^2}x_0^2 - 2x_0c + a^2} = \sqrt{(\frac{c}{a}x_0 - a)^2} = |ex_0 - a|\).
\(\because ex_0 - a < 0\).
\(\therefore |PF_2| = a - ex_0\).
\(|PF_1|\) 也是同理.
当然,如果是竖椭的话:
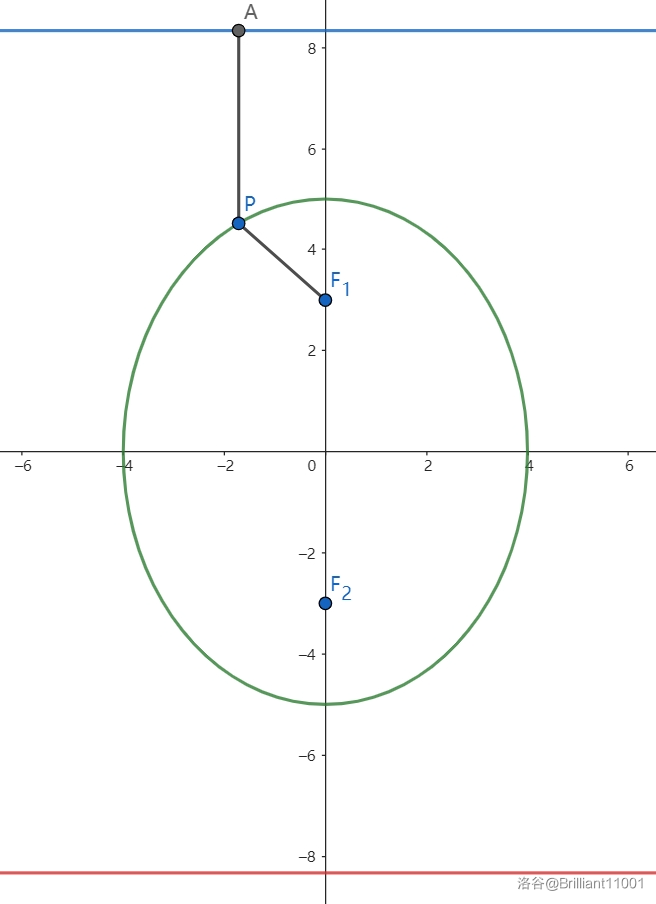
也有:\(\begin{cases}PF_1 = a - ey_0\\ PF_2 = a + ey_0\end{cases}\).
还有一个二级结论:设直线 \(PF_2\) 与 \(x\) 轴的正半轴夹角为 \(\theta\),则 \(\begin{cases}PF_1 = \frac{ep}{1 - e\cos\theta}\\PF_2 = \frac{ep}{1 + e\cos\theta}\end{cases}\).其中 \(p\) 为焦准距.
推导:
不妨先推 \(PF_2\) 这边的.
由第二定义得:\(PA = \frac{PF_2}{e}\).
\(\therefore p = PF_2\cos\theta + \frac{PF_2}{e}\).
整理得:\(PF_2 = \frac{ep}{1 + e\cos\theta}\).
\(PF_1\) 这边的也是同理.
其实说实话,我感觉这个结论比焦半径公式用的要多一点。
来看一道例题吧。
例 \(1\):已知椭圆 \(C:\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1(a > b > 0)\),左右焦点分别为 \(F_1, F_2\),\(P, Q\) 为 \(C\) 在第一象限的两个动点,且 \(\overrightarrow{PF_1} = \lambda\overrightarrow{QF_2}\),\(\angle{PF_1F_2} = \frac{\pi}{6}\),若 \(|PF_1| = 3|QF_2|\),则 \(C\) 的离心率为( )
\(A. \frac{\sqrt 3}{3}\space\space\space\space B. \frac{1}{2}\space\space\space\space C. \frac{\sqrt 5}{3}\space\space\space\space D. \frac{\sqrt 10}{4}\)
先讲一下第二定义的快捷法一:
\(PF_1 = \frac{ep}{1 + e\cos\frac{5}{6}\pi}, QF_2 = \frac{ep}{1 + e\cos\frac{\pi}{6}}\).
\(\because PF_1 = 3QF_2\).
\(\therefore\frac{ep}{1 + e\cos\frac{5}{6}\pi} = \frac{3ep}{1 + e\cos\frac{\pi}{6}}\Rightarrow e = \frac{\sqrt 3}{3}\).
是不是很高效?一道选择题压轴题只要 30s!
当然还有一种朴素的法二,是严格按照第一定义来做的:
设 \(QF_2 = x, QF_1 = 2a - x\).
\(PF_1 = 3x, PF_2 = 2a - 3x\). 然后在 \(\triangle{PF_1F_2}\) 和 \(\triangle{QF_1F_2}\) 中分别用一次余弦定理即可求出 \(a, c\) 之间的关系,可求出 \(e = \frac{\sqrt 3}{3}\).
第二种方法显然就不如第一种来的快了。
第三定义
平面内的动点到两定点的斜率乘积等于常数 \(-\frac{b^2}{a^2} = e^2 - 1\) 的点的轨迹。(是除掉该两顶点的椭圆)
推导:
设 \(A_1(-a, 0), A_2(a, 0)\) 两点为椭圆 \(C:\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1\) 的左右顶点,\(P(x, y)\) 在椭圆 \(C\) 上运动.
\(\therefore k_{PA_1} = \frac{y}{x + a}, k_{PA_2} = \frac{y}{x - a}\).
\(\therefore k_{PA_1}k_{PA_2} = \frac{y^2}{x^2 - a^2}\).
\(\because b^2x^2 + a^2y^2 = a^2b^2\).
\(\therefore y^2 = b^2(1 - \frac{1}{a^2}x^2)\).
\(\therefore \text{原式} = \frac{b^2(1 - \frac{1}{a^2}x^2)}{x^2 - a^2} = -\frac{b^2}{a^2}\).
这个结论可能出现在选择题中,见到就可以秒了。
这里我不推荐记忆 \(-\frac{b^2}{a^2}\),而是记忆 \(e^2 - 1\),因为双曲线的第三定义是 \(\frac{b^2}{a^2}\),但也是 \(e^2 - 1\)。若你记忆前者,可能会把椭圆和双曲线记混淆,但记忆 \(e^2 - 1\) 就可以一劳永逸了。
这里还关联了一个广义的圆周定理:若 \(A_1,A_2\) 是椭圆上关于原点对称的两点,对于不与她们重合的点 \(P(x, y)\),也有 \(k_{PA_1}k_{PA_2} = -\frac{b^2}{a^2}\).
推导和第三定义如出一辙,就不赘述。
来看一道有意思的题:
例 \(2\):已知椭圆 \(C:\frac{x^2}{2} + y^2 = 1\) 的左右顶点分别为 \(A, B\),点 \(M_1, M_2,\cdots,M_{10}\) 是 \(AB\) 的十一等分点,分别过这十点作斜率为 \(k(k\ne 0)\) 的一组平行线,交 \(C\) 于 \(P_1, P_2,\cdots,P_{20}\),则直线 \(AP_1, AP_2,\cdots,AP_{20}\) 这二十条直线的斜率乘积为( )
\(A. -\frac{1}{16}\space\space\space\space B. -\frac{1}{32}\space\space\space\space C. \frac{1}{64}\space\space\space\space D. \frac{1}{1024}\)
用到第三定义实际上是很好做的:
利用配凑的思想,这里我们把 \(AP_i(i = 1, 2,\cdots,10)\) 和 \(AP_{i + 10}\) 看作一组.
由于过 \(M_1,M_2\cdots,M_{10}\) 的直线相互平行,且这十个点等分椭圆的长轴.
故原式就是十组“圆周”直线的斜率乘积,即为 \((e^2 - 1)^{10} = \frac{1}{1024}\).
2. 其他概念
长轴: 横椭为 \(x\) 轴顶点组成的线段,竖椭为 \(y\) 轴顶点组成的线段,长度都为 \(2a\).
短轴: 横椭为 \(y\) 轴顶点组成的线段,竖椭为 \(x\) 轴顶点组成的线段,长度都为 \(2b\).
焦距: 两焦点之间的距离,为 \(2c\).
通径: 过焦点且垂直于长轴的弦。
3. 重要二级结论
(1) 通径长
椭圆的通径长为 \(\frac{2b^2}{a}\).
推导:
横坐标 \(c\) 代入椭圆解析式,得:
\[\frac{c^2}{a^2}+\frac{y^2}{b^2}=1\]得 \(y^2=b^2-b^2e^2\).
\(\because a^2 = b^2 + c^2\).
\(\therefore c^2 = a^2 - b^2\),椭圆离心率还可以表示成 \(e = \frac{c}{a} = \sqrt{\frac{c^2}{a^2}} = \sqrt{\frac{a^2 - b^2}{a^2}} = \sqrt{1 - \frac{b^2}{a^2}}\).
代入得:
\[\begin{aligned}y^2&=b^2-e^2b^2\\&=b^2-(1-\frac{b^2}{a^2})b^2\\&=\frac{b^4}{a^2}\\y&=\pm\frac{b^2}{a}\end{aligned}\]此时 \(d=2|y|=\frac{2b^2}{a}\).
(2) 中点弦
\(A(x_1, y_1), B(x_2, y_2)\) 为椭圆上两点,\(M\) 为弦 \(AB\) 的中点,那么直线 \(OM\) 与直线 \(AB\) 的斜率之积为 \(-\frac{b^2}{a^2} = e^2 - 1\).
推导:
用点差法.
将 \(A, B\) 代入 \(C\) 得:
\(\begin{cases}\frac{x_1^2}{a^2} + \frac{y_1^2}{b^2} = 1\\ \frac{x_2^2}{a^2} + \frac{y_2^2}{b^2} = 1\end{cases}\)
(1) - (2),得:
\(\frac{(x_1 + x_2)(x_1 - x_2)}{a^2} + \frac{(y_1 + y_2)(y_1 - y_2)}{b^2} = 0\).
整理得:\(\frac{y_1 + y_2}{x_1 + x_2}\cdot\frac{y_1 - y_2}{x_1 - x_2} = -\frac{b^2}{a^2} = e^2 - 1\).
\(\because M(\frac{x_1 + x_2}{2}, \frac{y_1 + y_2}{2})\).
\(\therefore\frac{y_1 + y_2}{x_1 + x_2} = k_{OM}\).
\(\therefore k_{OM}\cdot k_{AB} = -\frac{b^2}{a^2} = e^2 - 1\).
(3) 焦点三角形
椭圆的左右焦点 \(F_1,F_2\) 与椭圆上一点 \(P\) 组成的三角形 \(\triangle PF_1F_2\) 称作这个椭圆的焦点三角形。
本节中出现的角 \(\theta\) 若无特殊说明均指代 \(\angle F_1PF_2\).
关于边的一些取值范围
焦点三角形 \(\triangle PF_1F_2\) 中,\(|PF_1|\in(a - c, a + c),|PF_2|\in(a - c, a + c),|PF_1||PF_2|\le a^2\).
推导:
在 \(P\) 与左右端点重合时 \(PF_1, PF_2\) 取到最值,但是此时 \(P, F_1, F_2\) 三点共线,因此不是三角形,所以是开区间。
根据基本不等式,得: \(\(|PF_1||PF_2|\le\left(\frac{|PF_1| + |PF_2|}{2}\right)^2 = a^2\)\)
周长
焦点三角形 \(\triangle PF_1F_2\) 的周长 \(C_{\triangle PF_1F_2} = |PF_1| + |PF_2| + |F_1F_2| = 2a + 2c\).
推导:
根据椭圆的第一定义,得:\(PF_1 + PF_2 = 2a\).
\(\therefore C_{\triangle{PF_1PF_2}} = PF_1 + PF_2 + F_1F_2 = 2a + 2c\).
面积
\(\triangle PF_1F_2\) 的面积 \(S_{\triangle PF_1F_2} = b^2\tan\frac{\theta}{2}\).
推导:
根据第一定义和余弦定理,得:
\(\begin{cases}PF_1 + PF_2 = 2a\\ 4c^2 = PF_1^2 + PF_2^2 - 2PF_1PF_2\cos\theta\end{cases}\)
整理一下:\(4c^2 = (PF_1 + PF_2)^2 - 2PF_1PF_2(1 + \cos\theta)\).
得:\(PF_1PF_2 = \frac{2b^2}{1 + \cos\theta}\).
\(S_{\triangle{PF_1F_2}} = \frac{1}{2}\cdot\frac{2b^2\sin\theta}{1 + \cos\theta} = \frac{b^2\sin\theta}{1 + \cos\theta}\).
对她使用半角公式 \(tan{\frac{\theta}{2}} = \frac{\sin\theta}{1 + \cos\theta}\),得:
\(S_{\triangle{PF_1F_2}} = b^2\tan{\frac{\theta}{2}}\).
(4) 极点极线求切线和切点弦
求切线:
若点 \(A(x_0, y_0)\) 在椭圆上,则过点 \(A\) 的切线为:\(\frac{x_0x}{a^2} + \frac{y_0y}{b^2} = 1\).
推导:
法一(基础联立法):
- 当直线 \(l\) 的斜率不存在时:
则 \(x_0 = a, y_0 = 0, l:x = a\),满足.
- 当直线 \(l\) 的斜率存在时:
设 \(l:y - y_0 = k(x - x_0)\).
\(\therefore y = k(x - x_0) + y_0 = k_x + y_0 - kx_0\).
令 \(m = y_0 - kx_0\),则:\(l:y = kx + m\).
联立 \(\begin{cases}y = kx + m\\ b^2x_0^2 + a^2y_0^2 = a^2b^2\end{cases}\)
得:\((a^2k^2 + b^2)x^2 + 2a^2kmx + a^2m^2 - a^2b^2 = 0\).
令 \(\Delta = 0\),则:\(4a^2b^2(a^2k^2 + b^2 - m^2) = 0\).
解得:\(m^2 = a^2k^2 + b^2\),即 \(k = \frac{b^2}{a^2}\cdot\frac{x_0}{y_0}\).
代入,得:\(l:\frac{x_0x}{a^2} + \frac{y_0y}{b^2} = 1\).
法二(点差法):
设 \(Q(x_1, y_1)\).
将 \(P, Q\) 代入 \(C\) 得:
\(\begin{cases}\frac{x_0^2}{a^2} + \frac{y_0^2}{b^2} = 1 & (1)\\ \frac{x_1^2}{a^2} + \frac{y_1^2}{b^2} = 1 & (2)\end{cases}\)
\((1) - (2)\),得:
\(k_{PQ} = -\frac{b^2}{a^2}\frac{x_0 + x_1}{y_0 + y_1}\).
当 \(x_1\rightarrow x_0, y_1\rightarrow y_0\) 时:
\(k_{PQ}\rightarrow k_{\text{切}}\).
\(\therefore k_{\text{切}} = -\frac{b^2}{a^2}\cdot\frac{x_0}{y_0}\).
代入,得:\(l:\frac{x_0x}{a^2} + \frac{y_0y}{b^2} = 1\).
求切点弦:
结论:点 \(P(x_0, y_0)\) 在椭圆 \(\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1\) 外,则过 \(P\) 做抛物线的两条切线的切点的连线为 \(\frac{x_0x}{a^2} + \frac{y_0y}{b^2} = 1\).
推导:
设这两个切点分别为 \(A(x_1, y_1),B(x_2, y_2)\).
根据上面所推的切线方程,得:\(\begin{cases}\frac{x_1x}{a^2} + \frac{y_1y}{b^2} = 1\\ \frac{x_2x}{a^2} + \frac{y_2y}{b^2} = 1\end{cases}\)
\(\because P\) 为交点.
\(\therefore P\) 应该同时适用这两个方程,则有:\(\begin{cases}\frac{x_1x_0}{a^2} + \frac{y_1y_0}{b^2} = 1\\ \frac{x_2x_0}{a^2} + \frac{y_2y_0}{b^2} = 1\end{cases}\).
根据同构式的思想,\(x_1,x_2\) 为方程 \(\frac{x_0x}{a^2} + \frac{y_0y}{b^2} = 1\) 的两个根.
所以点 \(A,B\) 在直线 \(\frac{x_0x}{a^2} + \frac{y_0y}{b^2} = 1\) 上.
\(\texttt{0x02}\) 双曲线
0. 基本代数形式
横曲:\(C:\frac{x^2}{a^2} - \frac{y^2}{b^2} = 1(a > 0,b > 0)\),焦点在 \(x\) 轴上。
竖曲:\(C:\frac{y^2}{a^2} - \frac{x^2}{b^2} = 1(a > 0,b > 0)\),焦点在 \(y\) 轴上。
\(c^2 = a^2 + b^2,e > 1\).
1. 基本三大定义
和椭圆相似之处较多,故证明省略。
第一定义
与两个固定的点(叫做焦点)的距离差是常数的点的轨迹。
形式化的,若 \(||PF_1| - |PF_2|| = d = 2a\),则 \(P\) 的运动轨迹为双曲线。
这里要特别注意:得看是否加了绝对值,若有,则是双;若无,则是单。
第二定义
双曲线上的点到焦点的距离与到准线的距离之比为离心率,对双曲线来说,其准线为 \(x = \pm\frac{a^2}{c}\).
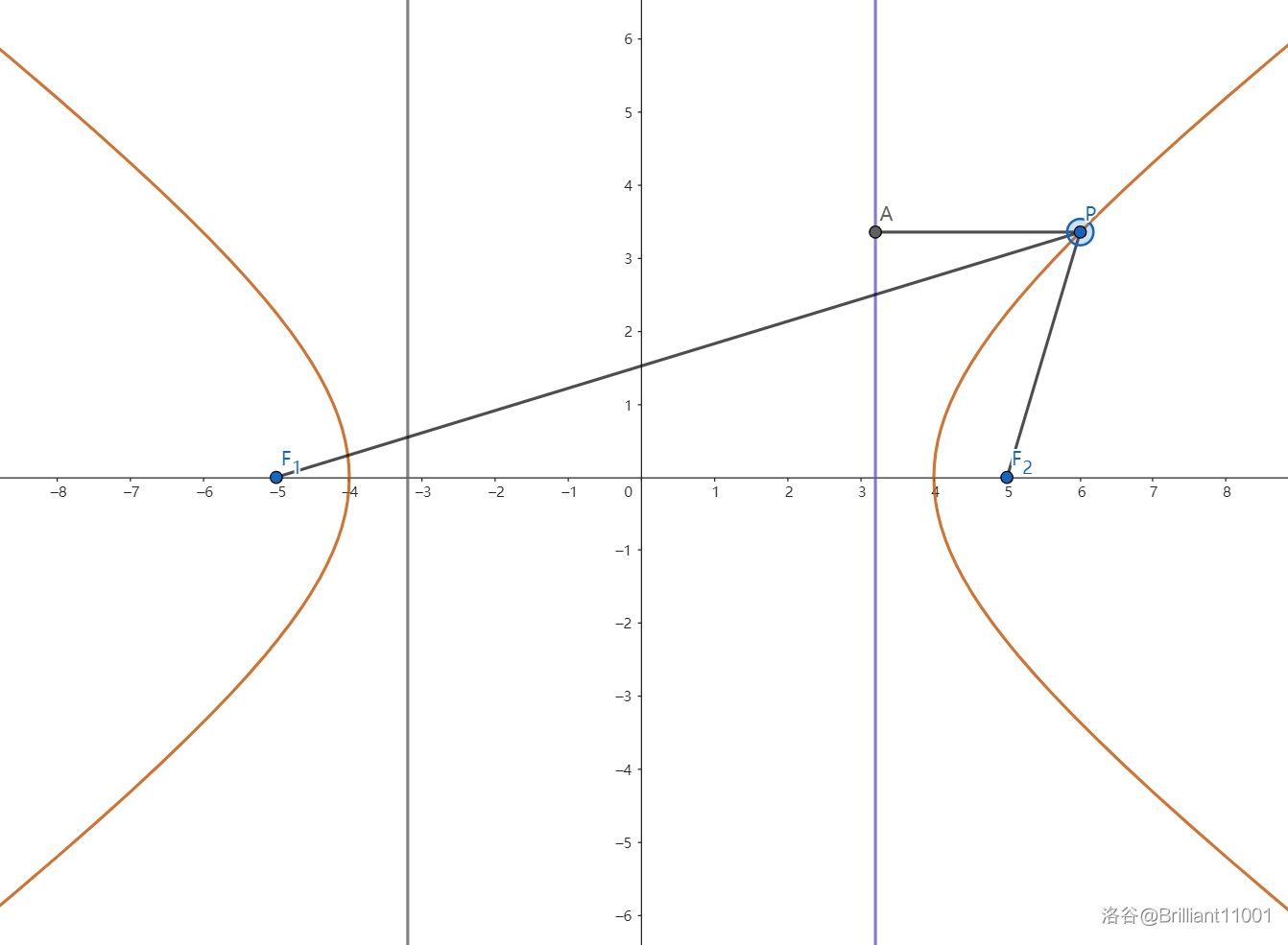
如图所示:其中 \(\frac{PF_2}{PA} = e\).
焦半径的推导和椭圆如出一辙,不再赘述,这里只给出结论:
设 \(P(x_0, y_0)\).
- 若 \(P\) 在右支
\(\begin{cases}PF_1 = ex_0 + a\\PF_2 = ex_0 - a\end{cases}\)
- 若 \(P\) 在左支
\(\begin{cases}PF_1 = -ex_0 - a\\PF_2 = -ex_0 + a\end{cases}\)
这个就比椭圆要难记忆一点了,我的建议是代入特殊点进行记忆。
另一个二级结论也相似,但有些许变化。
设直线 \(PF_2\) 与 \(x\) 轴的正半轴夹角为 \(\theta\),则 \(\begin{cases}PF_1 = \frac{ep}{1 + e\cos\theta}\\PF_2 = \frac{ep}{1 - e\cos\theta}\end{cases}\) 其中 \(p\) 为焦准距.
第三定义
平面内的动点到两定点的斜率乘积等于常数 \(\frac{b^2}{a^2} = e^2 - 1\) 的点的轨迹。(是除掉该两顶点的双曲线)
双曲线也满足广义圆周定理。
2. 其他概念
实轴:顶点组成的线段,长度都为 \(2a\).
虚轴:横曲为 \((0, \pm b)\) 组成的线段,竖曲为 \((\pm b, 0)\) 组成的线段,长度都为 \(2b\).
焦距:两焦点之间的距离,为 \(2c\).
通径:过焦点且垂直于长轴的弦。
渐近线:横曲为 \(y = \pm\frac{b}{a}x\),竖曲为 \(y = \pm\frac{a}{b}x\).
顺便一提,与双曲线 \(\frac{x^2}{a^2} - \frac{y^2}{b^2} = 1(a > 0, b > 0)\) 有共同渐近线的双曲线方程可表示为 \(\frac{x^2}{a^2} - \frac{y^2}{b^2} = t(t\ne 0)\).
而且如果一不小心忘记了渐近线的方程,也可以直接令双曲线方程等于零来解得。
3. 重要二级结论
(1) 通径长
通径长度为 \(\frac{2b^2}{a}\).
推导:
将横坐标 \(\pm c\) 代入得 \(y^2=b^2e^2-b^2\).
\(\because c^2 = a^2 + b^2\).
\(\therefore e = \sqrt{1 + \frac{b^2}{a^2}}\).
那么 \(y^2=\frac{b^4}{a^2}\),得 \(y=\pm\frac{2b^2}{a}\).
此时通径长为 \(d=2|y|=\frac{2b^2}{a}\).
(2) 焦准距
双曲线的焦点到其渐近线的距离为 \(b\).
推导:
右焦点 \(F_2(c, 0)\),到渐近线 \(y = \pm\frac{b}{a}x\) 的距离为: \(\(d=\dfrac{\frac{b}{a}c}{\sqrt{1+\frac{b^2}{a^2}}}=\dfrac{eb}{e}=b\)\)
(3) 中点弦
\(A(x_1, y_1), B(x_2, y_2)\) 为双曲线上两点,\(M\) 为弦 \(AB\) 的中点,那么直线 \(OM\) 与直线 \(AB\) 的斜率之积为 \(\frac{b^2}{a^2} = e^2 - 1\).
推导:
用点差法.
将 \(A, B\) 代入 \(C\) 得:
\(\begin{cases}\frac{x_1^2}{a^2} - \frac{y_1^2}{b^2} = 1 & (1)\\ \frac{x_2^2}{a^2} - \frac{y_2^2}{b^2} = 1 & (2)\end{cases}\)
\((1) - (2)\),得:
\(\frac{(x_1 + x_2)(x_1 - x_2)}{a^2} - \frac{(y_1 + y_2)(y_1 - y_2)}{b^2} = 0\).
整理得:\(\frac{y_1 + y_2}{x_1 + x_2}\cdot\frac{y_1 - y_2}{x_1 - x_2} = \frac{b^2}{a^2} = e^2 - 1\).
\(\because M(\frac{x_1 + x_2}{2}, \frac{y_1 + y_2}{2})\).
\(\therefore\frac{y_1 + y_2}{x_1 + x_2} = k_{OM}\).
\(\therefore k_{OM}\cdot k_{AB} = \frac{b^2}{a^2} = e^2 - 1\).
(4) 焦点三角形
双曲线的左右焦点 \(F_1, F_2\) 与双曲线上一点 \(P\) 组成的三角形 \(\triangle PF_1F_2\) 称作这个双曲线的焦点三角形。
本节中出现的角 \(\theta\) 若无特殊说明均指代 \(\angle F_1PF_2\).
周长
焦点三角形 \(\triangle{PF_1F_2}\) 的周长为 \({2}e|x_0|+2c\).
推导:
根据前面所证明的焦半径公式可得这个结论。
面积
焦点三角形 \(\triangle PF_1F_2\) 的面积为 \(\dfrac{b^2}{\tan\frac{\theta}{2}}=b^2\cot\frac{\theta}{2}\).
推导:
结合双曲线的对称性,我们只要考虑 \(P\) 在第一象限内的情形即可.
根据第一定义和余弦定理,得:
\(\begin{cases}PF_1 - PF_2 = 2a\\ 4c^2 = PF_1^2 + PF_2^2 - 2PF_1PF_2\cos\theta\end{cases}\)
整理一下:\(4c^2 = (PF_1 - PF_2)^2 + 2PF_1PF_2(1 - \cos\theta)\).
得:\(PF_1PF_2 = \frac{2b^2}{1 - \cos\theta}\).
\(S_{\triangle{PF_1F_2}} = \frac{1}{2}\cdot\frac{2b^2\sin\theta}{1 - \cos\theta} = \frac{b^2\sin\theta}{1 - \cos\theta}\).
对她使用半角公式 \(\cot{\frac{\theta}{2}} = \frac{\sin\theta}{1 - \cos\theta}\),得:
\(S_{\triangle{PF_1F_2}} = b^2\cot{\frac{\theta}{2}} = \frac{b^2}{\tan{\frac{\theta}{2}}}\).
内切圆
如图所示:
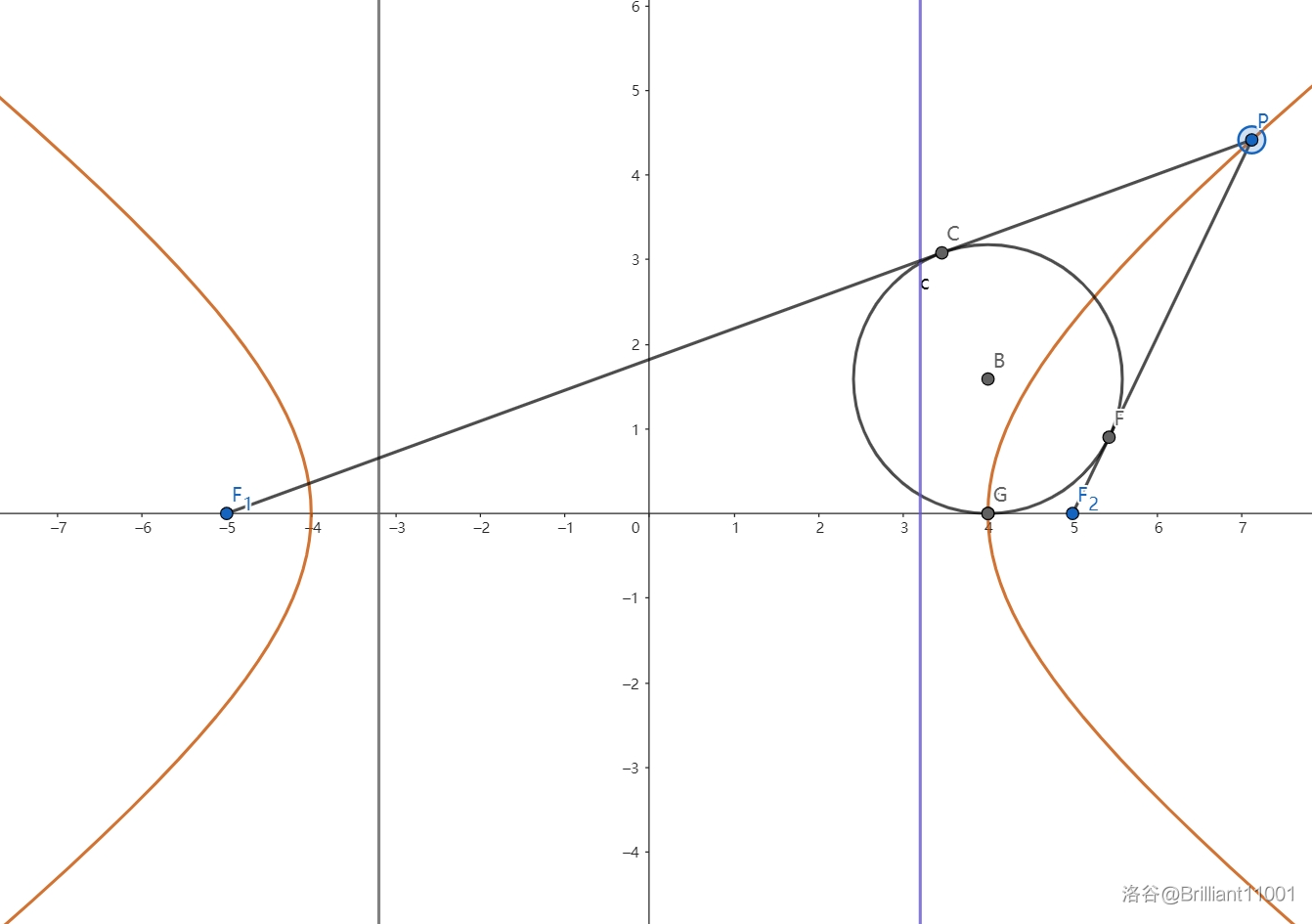
内切圆圆心 \(B\) 的横坐标为 \(a\).
推导:
设内切圆与 \(PF_1\) 相切于 \(C\),与 \(PF_2\) 相切于 \(F\),与 \(F_1F_2\) 相切于 \(G\).
\(PF_1 - PF_2 = CF_1 - FF_2 = GF_1 - GF_2 = c + x_G - c + x_G = 2x_G = 2a\).
\(\therefore x_G = a\).
(5) 梦幻联动:和椭圆共焦点问题
椭圆 \(C:\frac{x^2}{a_1^2} + \frac{y^2}{b_1^2} = 1\),双曲线 \(E:\frac{x^2}{a_2^2} - \frac{y^2}{b_2^2} = 1\) 共焦点 \(F_1, F_2\),离心率分别为 \(e_1, e_2\),设她们在第一象限交于点 \(P,\angle{F_1PF_2} = \theta\),则有 \(\frac{\sin^2{\frac{\theta}{2}}}{e_1^2} + \frac{\cos^2{\frac{\theta}{2}}}{e_2^2} = 1\).
推导:
法一(朴素余弦定理): 在 \(\triangle{PF_1PF_2}\) 中,根据余弦定理得:\(4c^2 = PF_1^2 + PF_2^2 - 2PF_1PF_2\cos\theta\).
这里有一个绝妙的转化:将 \(\cos\theta\) 用倍角公式转化为 \(\cos^2{\frac{\theta}{2}} - \sin^2{\frac{\theta}{2}}\),从而凑出两个完全平方.
\(\therefore 4c^2 = \cos^2{\frac{\theta}{2}}PF_1^2 + \sin^2{\frac{\theta}{2}}PF_1^2 + \cos^2{\frac{\theta}{2}}PF_2^2 + \sin^2{\frac{\theta}{2}}PF_2^2 - 2\cos^2{\frac{\theta}{2}}PF_1PF_2 + 2\sin^2{\frac{\theta}{2}}PF_1PF_2\).
\(\therefore 4c^2 = \cos^2{\frac{\theta}{2}}(PF_1^2 + PF_2^2 - 2PF_1PF_2) + \sin^2{\frac{\theta}{2}}(PF_1^2 + PF_2^2 + 2PF_1PF_2)\).
\(\therefore 4c^2 = \cos^2{\frac{\theta}{2}}(PF_1 - PF_2)^2 + \sin^2{\frac{\theta}{2}}(PF_1 + PF_2)^2\).
\(\therefore 4c^2 = 4a_2^2\cos^2{\frac{\theta}{2}} + 4a_1^2\sin^2{\frac{\theta}{2}}\).
两边同除以 \(4c^2\),得:
\(\frac{\sin^2{\frac{\theta}{2}}}{e_1^2} + \frac{\cos^2{\frac{\theta}{2}}}{e_2^2} = 1\).
法二(焦点三角形面积法):
\(S_{\triangle{PF_1F_2}} = b_1^2\tan{\frac{\theta}{2}} = \frac{b_2^2}{\tan{\frac{\theta}{2}}}\).
\(\therefore (a_1^2 - c^2)\tan^2{\frac{\theta}{2}} = (c^2 - a_2^2)\).
整理得:\(\frac{\sin^2{\frac{\theta}{2}}}{e_1^2} + \frac{\cos^2{\frac{\theta}{2}}}{e_2^2} = 1\).
用这个结论可以直接计算 \(e_1e_2\) 或 \(e_1^2 + e_2^2\) 最值。
例 \(3\):已知 \(F_1, F_2\) 为椭圆与双曲线的公共焦点,\(P\) 是她们的一个公共点,\(\angle{F_1PF_2} = \frac{\pi}{3}\),则椭圆与双曲线之积的最小值为( )
\(A. 2\sqrt 3\space\space\space\space B. 1\space\space\space\space C. \frac{\sqrt 3}{2}\space\space\space\space D. 2\)
根据上面推出的结论:\(\frac{sin^2{\frac{\pi}{6}}}{e_1^2} + \frac{\cos^2{\frac{\pi}{6}}}{e_2^2} = 1\).
整理得:\(4e_1^2e_2^2 = 3e_1^2 + e_2^2\).
要求 \(e_1e_2\) 的最小值,根据基本不等式得:\(4e_1^2e_2^2 = 3e_1^2 + e_2^2\ge 2\sqrt{3e_1^2e_2^2} = 2\sqrt 3 e_1e_2\).
\(\therefore e_1e_2\ge \frac{\sqrt 3}{2}\).
\(\texttt{0x03}\) 抛物线
0. 基本代数形式
横抛:\(\Gamma :y^2 = 2px\),若 \(p > 0\) 则开口朝右;若 \(p < 0\) 则开口朝左,其焦点为 \((\frac{p}{2}, 0)\),准线为 \(x = -\frac{p}{2}\).
竖抛:\(\Gamma :x^2 = 2py\),若 \(p > 0\) 则开口朝上;若 \(p < 0\) 则开口朝下,其焦点为 \((0, \frac{p}{2})\),准线为 \(y = -\frac{p}{2}\).
推荐记忆方式:看一次项,是什么就关于哪条轴对称。
\(e = 1\).
1. 基本定义
抛物线就没那么多定义了,所以简单得多。
平面内于一个定点 \(F\) 和一条直线 \(l\) 的距离相等的点的轨迹,\(F\) 叫做焦点,\(l\) 叫做准线。
2. 其他概念
通径:过焦点与对称轴垂直的弦,长度为 \(2p\).
焦半径:抛物线上一点 \(P(x, y)\) 到焦点 \(F(\frac{p}{2}, 0)\),的距离 \(|PF| = x + \frac{p}{2}\).
3. 重要二级结论
(1) 极点极线求切线和切点弦
求切线:
结论:点 \(P(x_0, y_0)\) 在抛物线 \(y^2 = 2px\) 上,则过 \(P\) 的切线为 \(y_0y = p(x + x_0)\).
推导:
设过点 \(P\) 点的直线为 \(y - y_0 = k(x - x_0)\).
联立 \(\begin{cases}y - y_0 = k(x - x_0)\\ y^2 = 2px\end{cases}\)
得:\(k^2y^2 - 2py + 2py_0 - 2pkx_0 = 0\).
令 \(\Delta = 0\),得关于 \(k\) 得二次函数:\(8px_0k^2 - 8py_0k + 4p^2 = 0\).
解得:\(k = \frac{y_0}{2x_0}\).
代入,得:\(y_0y = 2p\frac{x + x_0}{2} = p(x + x_0)\).
求切点弦:
结论:点 \(P(x_0, y_0)\) 在抛物线 \(y^2 = 2px\) 外,则过 \(P\) 做抛物线的两条切线的切点的连线为 \(y_0y = p(x + x_0)\).
推导:
设这两个切点分别为 \(A(x_1, y_1),B(x_2, y_2)\).
根据上面所推的切线方程,得:\(\begin{cases}y_1y = p(x + x_1)\\ y_2y = p(x + x_2)\end{cases}\)
\(\because P\) 为交点.
\(\therefore P\) 应该同时适用这两个方程,则有:\(\begin{cases}y_1y_0 = p(x_0 + x_1)\\ y_2y_0 = p(x_0 + x_2)\end{cases}\)
根据同构式的思想,\(x_1,x_2\) 为方程 \(y_0y = p(x + x_0)\) 的两个根.
所以点 \(A,B\) 在直线 \(y_0y = p(x + x_0)\) 上.
(2) 焦半径公式
若倾斜角为 \(\alpha\) 的直线 \(l\) 经过抛物线 \(y^2 = 2px(p > 0)\) 的焦点,且与抛物线相交于 \(A(x_1, y_1), B(x_2, y_2)(y_1 > y_2)\) 两点,则:
\(|AF| = x_1 + \frac{p}{2} = \frac{p}{1 - \cos\alpha},|BF| = x_2 + \frac{p}{2} = \frac{p}{1 + \cos\alpha}\).
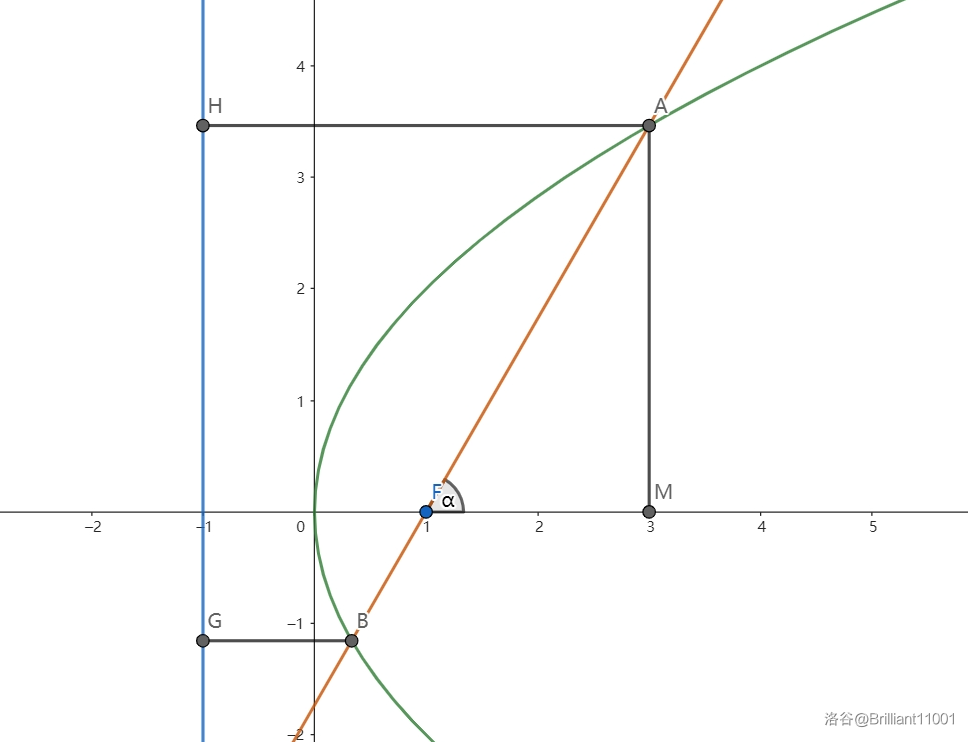
推导:
\(AF = AH + \frac{p}{2} + \frac{p}{2} + FM = p + AF\cos\alpha\).
\(\therefore AF = \frac{p}{1 - \cos\alpha}\).
同理:\(BF = \frac{p}{1 + \cos\alpha}\).
顺便还能推一个奇怪的公式:
\(\frac{1}{|AF|} + \frac{1}{|BF|} = \frac{2}{p}\).
推导:
原式 \(= \frac{1 - \cos\alpha}{p} + \frac{1 + cos\alpha}{p} = \frac{2}{p}\).
(3) 焦点弦长公式
\(|AB| = x_1 + x_2 + p = \frac{2p}{\sin^2\alpha}\).
推导:
\(AB = AF + BF = \frac{p}{1 - \cos\alpha} + \frac{p}{1 + \cos\alpha} = \frac{p(1 + \cos\alpha) + p(1 - \cos\alpha)}{1 - \cos^2\alpha} = \frac{2p}{\sin^2\alpha}\).
(4) 焦点弦三角形面积公式
\(S_{\triangle{OAB}} = \frac{p^2}{2\sin\alpha}\).
推导:
\(S_{\triangle{OAB}} = \frac{1}{2}OF(y_1 - y_2) = \frac{1}{2}\cdot\frac{p}{2}\cdot AB\sin\alpha = \frac{p}{4}\frac{2p}{\sin\alpha} = \frac{p^2}{2\sin\alpha}\).
(5) 坐标关系
\(x_1x_2 = \frac{p^2}{4},y_1y_2 = -p^2\).
推导:
可知直线 \(l\) 的斜率不为零,设 \(l:x = ty + \frac{p}{2}\).
联立 \(\begin{cases}x = ty + \frac{p}{2}\\ y^2 = 2px\end{cases}\)
得:\(y^2 - 2pty - p^2 = 0\).
\(\because\) 有两个交点.
\(\therefore \Delta > 0\).
\(\begin{cases}y_1 + y_2 = 2pt\\ y_1y_2 = -p^2\end{cases}\)
又 \(\because x_1 = \frac{y_1^2}{2p}, x_2 = \frac{y_2^2}{2p}\).
\(\therefore x_1x_2 = \frac{(y_1y_2)^2}{4p^2} = \frac{p^4}{4p^2} = \frac{p^2}{4}\).
(6) 焦点弦圆、焦半径圆
以 \(AB\) 为直径的圆与准线相切,以 \(AF\) 为直径的圆与 \(y\) 轴相切。
推导:
设 \(AB\) 中点 \(C(x_0, y_0)\).
半径 \(R = \frac{1}{2}AB = \frac{1}{2}(x_1 + x_2 + p) = x_0 + \frac{p}{2}\).
而 \(C\) 到准线的距离 \(d = x_0 + \frac{p}{2} = R\).
\(\therefore\) 以 \(AB\) 为直径的圆与准线相切.
设 \(AF\) 的中点 \(E(x_0, y_0)\).
半径 \(R = \frac{1}{2}AF = \frac{1}{2}(x_1 + \frac{p}{2})\).
而 \(E\) 到 \(y\) 轴的距离 \(d = \frac{1}{2}(x_1 + \frac{p}{2}) = R\).
\(\therefore\) 以 \(AF\) 为直径的圆与 \(y\) 轴相切.
(7) 两点斜率
设 \(A(x_1, y_1), B(x_2, y_2)\) 是抛物线 \(y^2 = 2px\) 上的两点,则 \(k_{AB} = \frac{2p}{y_1 + y_2}\).
推导:
\(A(\frac{y_1^2}{2p}, y_1), B(\frac{y_2^2}{2p}, y_2)\).
\(\large\therefore k_{AB} = \frac{y2 - y1}{\frac{y_2^2}{2p} - \frac{y_1^2}{2p}} = \frac{y_2 - y_1}{\frac{(y_2 + y_1)(y_2 - y_1)}{2p}} = \frac{2p}{y_1 + y_2}\).
\(\texttt{To be continued……}\)